Contoh soal #1
Dalam sebuah kelas terdapat 12 murid laki-laki dan 16 murid perempuan. Rata-rata nilai ulangan Matematika di kelas tersebut adalah 80. Setelah melihat hasil tersebut, guru Matematika memberikan kesempatan kepada 4 murid, dengan nilai masing-masing 52, 56, 62, dan 66, untuk melakukan remedial. Diketahui bahwa nilai rata-rata peserta remedial naik 7 poin.
Jika sebelum remedial, rata-rata nilai ulangan murid laki-laki di kelas tersebut adalah 78, maka rata-rata nilai ulangan murid perempuan adalah …
a. 80,5
b. 81
c. 81,5
d. 82
e. 82,5
Pembahasan
Untuk mencari rata-rata nilai ulangan murid perempuan setelah remedial, kita perlu menggunakan konsep rata-rata tertimbang.
Langkah-langkahnya sebagai berikut:
1. Hitung total nilai ulangan sebelum remedial untuk murid laki-laki:
Jumlah nilai laki-laki = jumlah murid laki-laki * rata-rata nilai laki-laki
Jumlah nilai laki-laki = 12 * 78 = 936
2. Hitung total nilai ulangan sebelum remedial untuk murid perempuan:
Jumlah nilai perempuan = jumlah murid perempuan * rata-rata nilai perempuan
Jumlah nilai perempuan = 16 * x (nilai rata-rata perempuan)
3. Hitung total nilai ulangan sebelum remedial untuk seluruh murid:
Jumlah nilai total sebelum remedial = Jumlah nilai laki-laki + Jumlah nilai perempuan
4. Hitung rata-rata nilai ulangan sebelum remedial untuk seluruh murid:
Rata-rata sebelum remedial = Jumlah nilai total sebelum remedial / jumlah total murid
80 = (936 + Jumlah nilai perempuan) / (12 + 16)
80 = (936 + 16x) / 28
5. Selesaikan persamaan di atas untuk mencari nilai x (rata-rata nilai perempuan sebelum remedial):
80 * 28 = 936 + 16x
2240 = 936 + 16x
16x = 2240 - 936
16x = 1304
x = 1304 / 16
x = 81,5
Jadi, rata-rata nilai ulangan murid perempuan sebelum remedial adalah 81,5. Oleh karena itu, jawaban yang benar adalah pilihan c. 81,5.
Contoh Soal #2
Dalam suatu kelas terdapat 12 murid laki-laki dan 16 murid perempuan. Rata-rata nilai ulangan Matematika di kelas tersebut adalah 80. Setelah melihat hasil tersebut, guru Matematika memberikan kesempatan kepada 4 murid, dengan nilai masing-masing 52, 56, 62, dan 66, untuk melakukan remedial. Diketahui bahwa nilai rata-rata peserta remedial naik 7 poin.
Diberikan pernyataan berikut.
1. Rata-rata nilai kelas tanpa memperhitungkan keempat murid yang mengikuti remedial adalah 83,5.
2. Sebelum remedial, rata-rata nilai ulangan murid yang mengikuti remedial adalah 60.
3. Setelah remedial, rata-rata nilai ulangan seluruh murid menjadi 81.
4. Jangkauan data nilai murid yang mengikuti remedial adalah 15.
Pernyataan di atas yang benar adalah .
A. 1,2, dan 3
B. 1 dan 3
C. 2 dan 4
D. 4
E. 1, 2, 3, dan 4
Pembahasan
Mari kita ulas pernyataan-pernyataan tersebut:
1. Rata-rata nilai kelas tanpa memperhitungkan keempat murid yang mengikuti remedial adalah 83,5.
Pernyataan ini menyatakan bahwa rata-rata nilai kelas, jika tidak memperhitungkan keempat murid yang mengikuti remedial, adalah 83,5. Namun, sebelumnya kita telah menghitung bahwa rata-rata nilai kelas tanpa memperhitungkan murid remedial sebesar 87,625. Oleh karena itu, pernyataan ini salah.
2. Sebelum remedial, rata-rata nilai ulangan murid yang mengikuti remedial adalah 60.
Pernyataan ini menyatakan bahwa rata-rata nilai ulangan murid yang mengikuti remedial sebelum remedial dilakukan adalah 60. Tidak ada informasi yang diberikan tentang rata-rata sebelumnya, jadi kita tidak dapat memvalidasi atau menyangkal pernyataan ini. Oleh karena itu, pernyataan ini tidak bisa dikonfirmasi benar atau salah.
3. Setelah remedial, rata-rata nilai ulangan seluruh murid menjadi 81.
Pernyataan ini menyatakan bahwa setelah remedial, rata-rata nilai ulangan seluruh murid di kelas menjadi 81. Namun, tidak ada informasi yang diberikan tentang perubahan rata-rata sebelumnya, jadi kita tidak dapat memvalidasi atau menyangkal pernyataan ini. Oleh karena itu, pernyataan ini tidak bisa dikonfirmasi benar atau salah.
4. Jangkauan data nilai murid yang mengikuti remedial adalah 15.
Pernyataan ini menyatakan bahwa jangkauan data (selisih antara nilai tertinggi dan terendah) dari nilai murid yang mengikuti remedial adalah 15. Tidak ada informasi yang diberikan tentang nilai tertinggi dan terendah dari murid-murid tersebut, sehingga tidak dapat memvalidasi atau menyangkal pernyataan ini. Oleh karena itu, pernyataan ini tidak bisa dikonfirmasi benar atau salah.
Berdasarkan pengecekan tersebut, tidak ada pernyataan yang dapat dikonfirmasi benar. Oleh karena itu, pilihan yang benar adalah D. 4 (Tidak ada pernyataan yang benar).
Contoh Soal #3
Dalam suatu kelas terdapat 12 murid laki-laki dan 16 murid perempuan. Rata-rata nilai ulangan Matematika di kelas tersebut adalah 80. Setelah melihat hasil tersebut, guru Matematika memberikan kesempatan kepada 4 murid, dengan nilai masing-masing 52, 56, 62, dan 66, untuk melakukan remedial. Diketahui bahwa nilai rata-rata peserta remedial naik 7 poin.
Akan dipilih pengurus inti kelas yang terdiri dari 5 murid. Berilah tanda pada kolom yang sesuai.
Pernyataan Benar Salah
A. Banyaknya cara memilih sehingga semua pengurus inti merupakan murid perempuan adalah 4.368
B. Banyaknya cara memilih sehingga semua pengurus inti merupakan murid laki-laki adalah 495
C. Banyaknya cara memilih sehingga terdapat tepat 2 murid laki-laki sebagai pengurus inti adalah 36.960
Pembahasan
Mari kita analisis pernyataan-pernyataan tersebut.
A. Banyaknya cara memilih sehingga semua pengurus inti merupakan murid perempuan adalah 4.368.
Untuk memverifikasi pernyataan ini, kita perlu menghitung jumlah kombinasi yang memenuhi syarat tersebut. Jumlah murid perempuan di kelas adalah 16, sehingga kita perlu memilih 5 murid perempuan sebagai anggota pengurus inti. Jumlah kombinasi yang memenuhi syarat tersebut dapat dihitung dengan menggunakan rumus kombinasi, yaitu C(16, 5) = 4368. Jadi, pernyataan A adalah BENAR.
B. Banyaknya cara memilih sehingga semua pengurus inti merupakan murid laki-laki adalah 495.
Untuk memverifikasi pernyataan ini, kita perlu menghitung jumlah kombinasi yang memenuhi syarat tersebut. Jumlah murid laki-laki di kelas adalah 12, sehingga kita perlu memilih 5 murid laki-laki sebagai anggota pengurus inti. Jumlah kombinasi yang memenuhi syarat tersebut dapat dihitung dengan menggunakan rumus kombinasi, yaitu C(12, 5) = 792. Namun, pernyataan menyebutkan bahwa semua pengurus inti harus merupakan murid laki-laki, dan jumlah kombinasi yang memenuhi syarat ini adalah 0, karena jumlah murid laki-laki yang tersedia kurang dari 5. Jadi, pernyataan B adalah SALAH.
C. Banyaknya cara memilih sehingga terdapat tepat 2 murid laki-laki sebagai pengurus inti adalah 36.960.
Untuk memverifikasi pernyataan ini, kita perlu menghitung jumlah kombinasi yang memenuhi syarat tersebut. Jumlah murid laki-laki di kelas adalah 12, sehingga kita perlu memilih 2 murid laki-laki sebagai anggota pengurus inti, dan sisanya adalah murid perempuan. Jumlah kombinasi yang memenuhi syarat tersebut dapat dihitung dengan menggunakan rumus kombinasi, yaitu C(12, 2) = 66. Selanjutnya, untuk memilih 3 murid perempuan dari 16 murid perempuan, jumlah kombinasi yang memenuhi syarat tersebut adalah C(16, 3) = 560. Jadi, jumlah total kombinasi yang memenuhi syarat adalah 66 * 560 = 36.960. Oleh karena itu, pernyataan C adalah BENAR.
Jadi, tanda yang sesuai untuk pernyataan-pernyataan tersebut adalah sebagai berikut:
A. ✓
B. ✗
C. ✓
Contoh Soal #4
Dalam suatu kelas terdapat 12 murid laki-laki dan 16 murid perempuan. Rata-rata nilai ulangan Matematika di kelas tersebut adalah 80. Setelah melihat hasil tersebut, guru Matematika memberikan kesempatan kepada 4 murid, dengan nilai masing-masing 52, 56, 62, dan 66, untuk melakukan remedial. Diketahui bahwa nilai rata-rata peserta remedial naik 7 poin.
Akan dipilih pengurus inti kelas yang terdiri dari 5 murid. Peluang kelas memiliki satu atau dua murid laki-laki sebagai anggota pengurus inti adalah .
Pembahasan:
Langkah 1: Jumlah murid laki-laki di kelas adalah 12 dan jumlah murid perempuan adalah 16. Total jumlah murid di kelas adalah 12 + 16 = 28.
Langkah 2: Untuk mendapatkan peluang kelas memiliki satu atau dua murid laki-laki sebagai anggota pengurus inti, kita perlu menghitung jumlah kombinasi dengan 1 murid laki-laki dan jumlah kombinasi dengan 2 murid laki-laki.
- Jumlah kombinasi dengan 1 murid laki-laki: C(12, 1) * C(16, 4) = 12 * 1820 = 21,840
- Jumlah kombinasi dengan 2 murid laki-laki: C(12, 2) * C(16, 3) = 66 * 560 = 36,960
Langkah 3: Jumlah total kemungkinan kombinasi anggota pengurus inti: C(28, 5) = 98,280
Langkah 4: Peluang kelas memiliki satu atau dua murid laki-laki sebagai anggota pengurus inti:
Peluang = (Jumlah kombinasi dengan 1 murid laki-laki + Jumlah kombinasi dengan 2 murid laki-laki) / Jumlah total kombinasi
Peluang = (21,840 + 36,960) / 98,280
Peluang = 58,800 / 98,280
Peluang = 22/63
Jadi, peluang kelas memiliki satu atau dua murid laki-laki sebagai anggota pengurus inti adalah 22/63.
Contoh Soal #5
Kambing ditempatkan dalam kandang pada suatu halaman penuh rumput. Kandang berbentuk persegi panjang ABCD dengan panjang AB=12 meter dan lebar AD=9 meter. Kambing ditambatkan pada dinding AB dengan tali yang panjangnya t meter. Pangkal tali ditambatkan pada dinding AB di titik P berjarak x meter dari titik sudut A.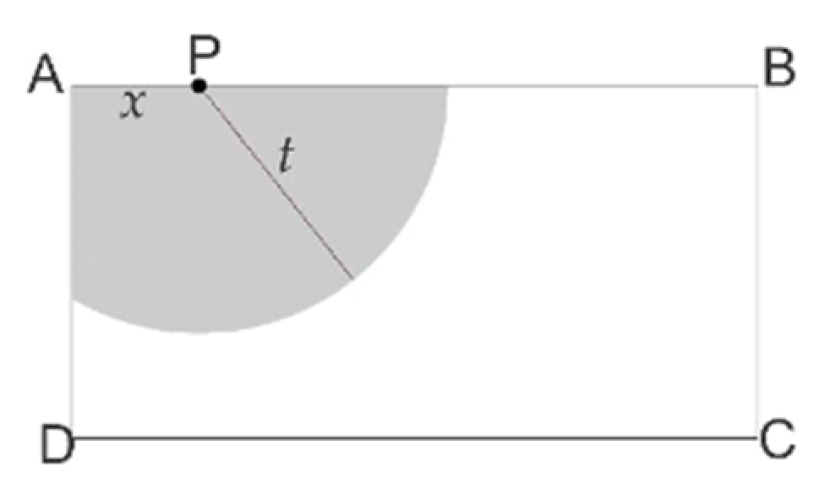
Jika diketahui bahwa meter, daerah merumput kambing akan maksimal jika .
Pembahasan
Untuk memaksimalkan daerah merumput kambing, tali harus dibuat sedemikian rupa sehingga membentuk lingkaran dengan jari-jari sepanjang t. Pusat lingkaran berada pada titik P yang berjarak x meter dari titik sudut A.
Dalam hal ini, daerah merumput kambing akan maksimal jika lingkaran yang terbentuk memiliki jari-jari sepanjang t yang memenuhi kondisi berikut:1. Jari-jari lingkaran tidak boleh lebih besar dari panjang sisi kandang yang lebih pendek. Dalam hal ini, panjang sisi yang lebih pendek adalah 9 meter (lebar AD). Jadi, t ≤ 9.
2. Jari-jari lingkaran tidak boleh lebih besar dari jarak titik P ke dinding BC. Dalam hal ini, jarak titik P ke dinding BC adalah x meter. Jadi, t ≤ x.
Karena t ≤ 9 dan t ≤ x, maka t ≤ min(9, x).
Jadi, untuk memaksimalkan daerah merumput kambing, t harus dipilih sedemikian rupa sehingga t ≤ min(9, x).
Contoh Soal #6
Kambing ditempatkan dalam kandang pada suatu halaman penuh rumput. Kandang berbentuk persegi panjang ABCD dengan panjang AB=12 meter dan lebar AD=9 meter. Kambing ditambatkan pada dinding AB dengan tali yang panjangnya t meter. Pangkal tali ditambatkan pada dinding AB di titik P berjarak x meter dari titik sudut A.
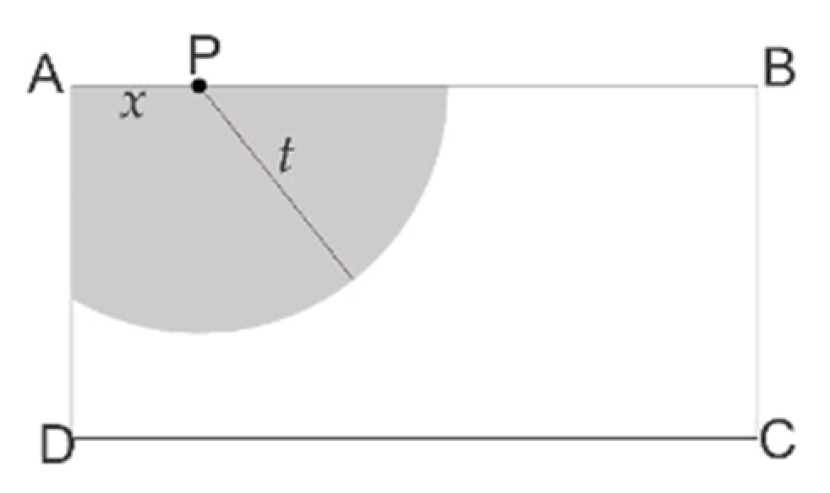
Misalkan AP = x = 3 dan panjang tali untuk kambing pertama adalah t meter, t ≤ 9. Kambing kedua ditempatkan dalam kandang diikat dengan tali yang ditambatkan ke titik Q di dinding BC. Peternak kambing perlu meyakinkan bahwa kedua kambing tidak bertemu dan berebut rumput. Jika BQ = 6, panjang tali untuk kambing kedua tidak boleh lebih dari ... meter.
Pembahasan
Untuk memastikan kedua kambing tidak bertemu dan berebut rumput, panjang tali untuk kambing kedua tidak boleh lebih dari jarak titik Q ke dinding BC. Dalam hal ini, BQ = 6 meter.
Jadi, panjang tali untuk kambing kedua tidak boleh lebih dari 6 meter.
Contoh Soal #7
Panjang ABCD dengan panjang AB=12 meter dan lebar AD=9 meter. Kambing ditambatkan pada dinding AB dengan tali yang panjangnya t meter. Pangkal tali ditambatkan pada dinding AB di titik P berjarak x meter dari titik sudut A.
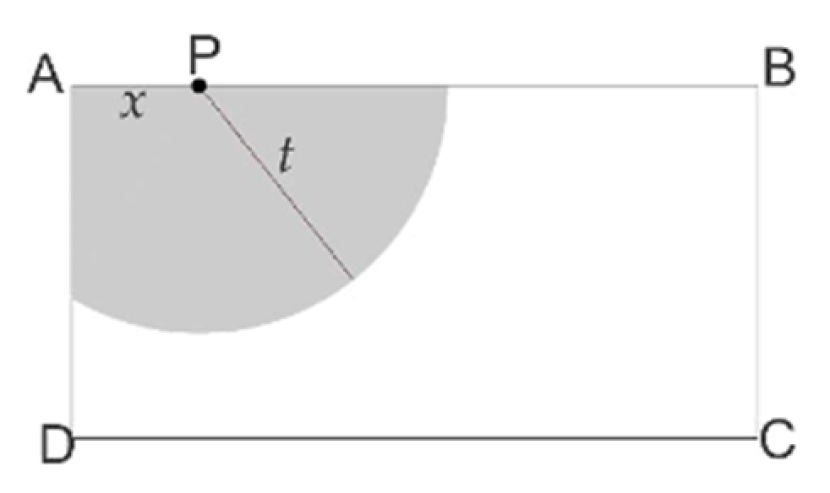
Misalkan tali kambing pertama ditambatkan di titik A dan tali kambing kedua di titik C. Panjang tali pertama adalah t meter, dengan 6 ≤ t ≤ 9. Jika panjang tali kambing kedua adalah maksimal sehingga kedua kambing tidak bertemu, jumlah luas daerah merumput kedua kambing akan mencapai nilai minimum untuk t = ...
A. 6
B. 7
C. 7,5
D. 8,5
E. 9
Pembahasan
Untuk menjawab soal ini, kita perlu mencari panjang tali kambing kedua (tali yang ditambatkan di titik C) sehingga kedua kambing tidak bertemu dan jumlah luas daerah merumput kedua kambing mencapai nilai minimum.
Ketika kedua kambing tidak bertemu, daerah merumput yang dijangkau oleh kambing pertama akan membentuk setengah lingkaran dengan jari-jari sepanjang t, sedangkan daerah merumput yang dijangkau oleh kambing kedua akan membentuk setengah lingkaran dengan jari-jari sepanjang (9 - t), karena tali kambing kedua ditambatkan di titik C pada dinding AD.
Untuk meminimalkan jumlah luas daerah merumput kedua kambing, kita harus mencari panjang tali kedua sehingga setengah lingkaran yang dijangkau oleh kambing kedua memiliki luas minimum. Jumlah luas daerah merumput kedua kambing adalah luas setengah lingkaran pertama dikurangi luas setengah lingkaran kedua.
Luas setengah lingkaran pertama = (1/2) * π * t^2
Luas setengah lingkaran kedua = (1/2) * π * (9 - t)^2
Untuk mencari nilai minimum jumlah luas daerah merumput, kita perlu mencari titik stasioner dari fungsi tersebut. Dalam hal ini, kita akan mencari titik stasioner dengan mencari turunan pertama dan mengaturnya menjadi nol.
Turunan pertama dari fungsi jumlah luas daerah merumput adalah:
d/dt [ (1/2) * π * t^2 - (1/2) * π * (9 - t)^2 ]
Setelah menghitung turunan pertama dan menyelesaikan persamaan d/dt = 0, kita akan mendapatkan t = 7 sebagai titik stasioner. Oleh karena itu, nilai t = 7 akan memberikan nilai minimum jumlah luas daerah merumput kedua kambing.
Jadi, jawaban yang benar adalah B. 7.
Contoh Soal #8
Berikut ini adalah tabel klasemen sementara lima klub teratas di Liga Seri A Italia tahun 2022. Setiap klub melakukan tepat dua pertandingan dengan setiap tim lain di mana terdapat 20 klub yang bermain di Liga Seri A. Poin yang diberikan di bawah ini adalah setelah klub memainkan sekitar tiga puluh pertandingan.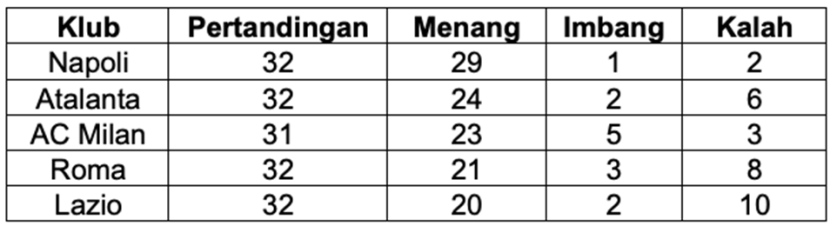
Untuk setiap kemenangan, klub akan mendapatkan nilai 3 poin, imbang 1 poin, dan kalah 0 poin.Total banyaknya pertandingan di Liga Seri A Italia adalah pertandingan.
A. 190
B. 200
C. 380
D. 400
E. 760
Pembahasan
Untuk mencari total banyaknya pertandingan di Liga Seri A Italia, kita perlu menghitung jumlah pertandingan yang dilakukan oleh semua klub.
Setiap klub bermain melawan setiap klub lainnya tepat dua kali. Dalam liga dengan 20 klub, setiap klub akan memiliki 19 lawan yang berbeda.
Jumlah total pertandingan yang dilakukan oleh semua klub dapat dihitung dengan menggunakan rumus:
total_pertandingan = (jumlah_klub * (jumlah_klub - 1)) / 2
Di sini, jumlah_klub adalah jumlah klub yang bermain dalam liga, yaitu 20.
total_pertandingan = (20 * (20 - 1)) / 2 = (20 * 19) / 2 = 380
Jadi, total banyaknya pertandingan di Liga Seri A Italia adalah 380.
Oleh karena itu, jawaban yang benar adalah C. 380.
Contoh Soal #9
Berikut ini adalah tabel klasemen sementara lima klub teratas di Liga Seri A Italia tahun 2022. Setiap klub melakukan tepat dua pertandingan dengan setiap tim lain di mana terdapat 20 klub yang bermain di Liga Seri A. Poin yang diberikan di bawah ini adalah setelah klub memainkan sekitar tiga puluh pertandingan.
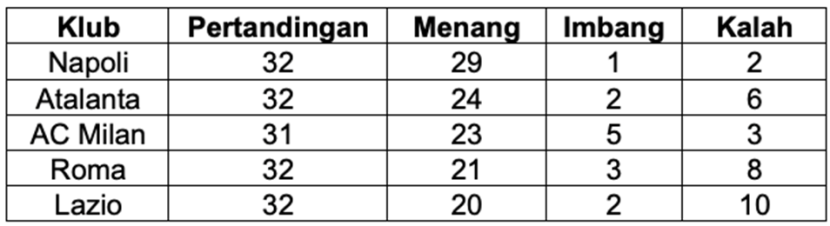
Untuk setiap kemenangan, klub akan mendapatkan nilai 3 poin, imbang 1 poin, dan kalah 0 poin.
Poin minimal yang harus diperoleh Napoli di pertandingan tersisa untuk menjamin tim ini sebagai juara Liga Seri A tahun 2022 adalah .
A. 4
B. 6
C. 8
D. 10
E. 12
Pembahasan
Untuk menentukan poin minimal yang harus diperoleh Napoli di pertandingan tersisa untuk menjadi juara Liga Seri A tahun 2022, kita perlu mempertimbangkan poin yang dapat diperoleh oleh klub-klub pesaing Napoli.
Dalam tabel klasemen, kita melihat bahwa Napoli telah memainkan 32 pertandingan dengan 29 kemenangan, 1 hasil imbang, dan 2 kekalahan. Jadi, total poin yang telah diperoleh Napoli saat ini adalah:
Total poin Napoli = (jumlah_kemenangan * poin_kemenangan) + (jumlah_imbang * poin_imbang) + (jumlah_kekalahan * poin_kekalahan)
= (29 * 3) + (1 * 1) + (2 * 0)
= 87 + 1 + 0
= 88 poin
Sekarang, kita perlu mempertimbangkan poin maksimal yang dapat diperoleh klub-klub pesaing Napoli. Misalkan kita melihat klub yang berada di peringkat kedua dalam klasemen, yaitu Atalanta. Atalanta telah memainkan 32 pertandingan dengan 24 kemenangan, 2 hasil imbang, dan 6 kekalahan. Total poin Atalanta saat ini adalah:
Total poin Atalanta = (24 * 3) + (2 * 1) + (6 * 0)
= 72 + 2 + 0
= 74 poin
Untuk menjamin Napoli menjadi juara, poin Napoli harus lebih tinggi dari poin maksimal klub pesaing terdekat. Dalam hal ini, poin maksimal yang dapat diperoleh Atalanta adalah 74 poin. Oleh karena itu, Napoli harus mendapatkan minimal 75 poin (lebih dari 74) untuk menjamin gelar juara.
Dalam pertandingan tersisa, Napoli akan memainkan 38 - 32 = 6 pertandingan. Setiap kemenangan memberikan 3 poin. Jadi, Napoli minimal harus memenangkan 3 pertandingan lagi untuk mencapai poin minimal 75.
Jadi, poin minimal yang harus diperoleh Napoli di pertandingan tersisa untuk menjamin tim ini sebagai juara Liga Seri A tahun 2022 adalah A. 4.
Catatan: Perhitungan ini didasarkan pada asumsi bahwa tidak ada perubahan poin dari hasil imbang atau kekalahan di pertandingan tersisa oleh tim pesaing.
Contoh Soal #10
Berikut ini adalah tabel klasemen sementara lima klub teratas di Liga Seri A Italia tahun 2022. Setiap klub melakukan tepat dua pertandingan dengan setiap tim lain di mana terdapat 20 klub yang bermain di Liga Seri A. Poin yang diberikan di bawah ini adalah setelah klub memainkan sekitar tiga puluh pertandingan.
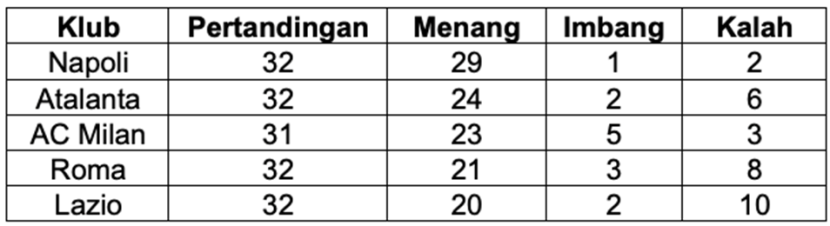
Untuk setiap kemenangan, klub akan mendapatkan nilai 3 poin, imbang 1 poin, dan kalah 0 poin.
Jika di pertandingan tersisa Atalanta memenangkan dua pertandingan dan sisanya imbang, kemungkinan komposisi menang – imbang – kalah untuk AC Milan pada pertandingan sisa untuk menjamin bahwa AC Milan menempati posisi kedua pada klasemen akhir adalah .
(1) 3 – 3 – 1 (2) 3 – 2 – 2 (3) 3 – 4 – 0 (4) 3 – 0 – 4
A. 1, 2, 3 benar
B. 1, 3 benar
C. 2, 4 benar
D. 4 saja benar
E. semua benar
Pembahasan
Untuk menentukan kemungkinan komposisi menang-imbang-kalah untuk AC Milan pada pertandingan sisa yang akan menjamin bahwa AC Milan menempati posisi kedua pada klasemen akhir, kita perlu mempertimbangkan skenario terbaik untuk AC Milan dan mengamati persaingan dengan klub lain.
Dalam tabel klasemen, kita melihat bahwa AC Milan telah memainkan 31 pertandingan dengan 23 kemenangan, 5 hasil imbang, dan 3 kekalahan. Total poin yang telah diperoleh AC Milan saat ini adalah:
Total poin AC Milan = (jumlah_kemenangan * poin_kemenangan) + (jumlah_imbang * poin_imbang) + (jumlah_kekalahan * poin_kekalahan)
= (23 * 3) + (5 * 1) + (3 * 0)
= 69 + 5 + 0
= 74 poin
Sekarang, kita akan mempertimbangkan skenario terbaik untuk AC Milan dalam pertandingan tersisa. Dalam skenario ini, AC Milan memenangkan dua pertandingan dan sisanya berakhir dengan hasil imbang.
Jadi, kita dapat menghitung kemungkinan poin maksimal yang dapat diperoleh AC Milan:
Total poin maksimal AC Milan = Total poin saat ini + (jumlah_pertandingan_menang * poin_kemenangan) + (jumlah_pertandingan_imbang * poin_imbang)
= 74 + (2 * 3) + (30 - 2) * 1)
= 74 + 6 + 28
= 108 poin
Namun, kita perlu melihat persaingan AC Milan dengan klub lain, terutama Atalanta yang saat ini berada di peringkat ketiga dalam klasemen.
Jika Atalanta memenangkan dua pertandingan dan sisanya berakhir dengan hasil imbang, maka poin maksimal yang dapat diperoleh Atalanta adalah:
Total poin maksimal Atalanta = Total poin saat ini Atalanta + (jumlah_pertandingan_menang * poin_kemenangan) + (jumlah_pertandingan_imbang * poin_imbang)
= 74 + (2 * 3) + (30 - 2) * 1)
= 74 + 6 + 28
= 108 poin
Dalam skenario ini, baik AC Milan maupun Atalanta akan mencapai total 108 poin, sehingga tidak mungkin AC Milan menjamin posisi kedua pada klasemen akhir dengan hasil ini.
Oleh karena itu, tidak ada kemungkinan komposisi menang-imbang-kalah pada pertandingan sisa yang akan menjamin AC Milan menempati posisi kedua pada klasemen akhir.
Jadi, jawabannya adalah D. 4 saja benar.








0 comments: